제가 요즘 수학에 빠져가지고 수학 강의를 듣는데 너무 재밌네요
수학에 재미를 붙이면 아마 수학이 쉬워지실겁니다.
그래도 수학은 어렵지만 재밌다고 생각하면 재밌어요!
오늘은 코사인 법칙의 증명법을 알아보도록 하겠습니다.
(2015개정교육과정 기준 고등학교 교육과정 중 수학 1에 나오는 내용입니다.)
삼각함수를 알고 계시다면 이해 하는 데는 큰 무리가 없을 거라 생각합니다만 삼각함수를 모르고 계시더라도
최소 삼각비 정도는 알고계셔야 이해가 될 거라 생각합니다.
그렇다면 먼저 코사인 법칙 내용부터 알아보겠습니다.
1)공식
-1. 코사인 제 1법칙의 내용은 다음과 같습니다.
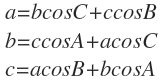
-2. 코사인 제 2법칙의 내용은 다음과 같습니다.
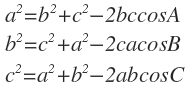
2)증명
-1. 제 1 코사인 법칙 증명
삼각형ABC의 꼭짓점 A의 대변 BC 혹은 그 연장선 상에 내린 수선의 발을 H라 하자.
(1) 삼각형 ABC가 예각삼각형일때

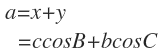
(2) 삼각형 ABC가 둔각삼각형일때


(3) 삼각형 ABC가 직각삼각형 일때


cosC는 0이므로
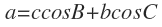
나머지 두 식에 대한 증명은 같은 방법으로 증명이 가능하므로 생략
-2. 제 2 코사인 법칙 증명
제 1 코사인 법칙의 첫번째 식에 a, 두번째 식에 b, 세번째 식에 c를 곱하면

첫번째 식에서 두번째와 세번째 식을, 두번째 식에서 첫번째와 세번째 식을. 세번쩨 식에서 첫번째와 두번째 식을 빼면
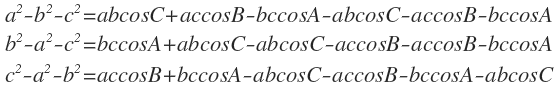
정리하면
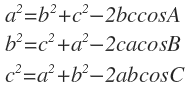
저도 배우고 있는 입장이라 완벽하지 않은 점 양해부탁드립니다.(오류/오타 지적 환영합니다.)
이 공식은 제가 처음 봤을때 뭐지? 했던 공식이기도 합니다.
헤론의 공식을 증명하는데 쓰인다고 들었을때도 의아해하기도 했습니다.
이 공식도 피타고라스의 정리보다는 아니지만 증명방법이 꽤 있는 공식입니다.
다음번에는 피타고라스의 정리와 제 2 코사인 법칙으로 증명이 가능한
헤론의 공식의 증명법을 포스팅하도록 하겠습니다.
공부하면서 궁금한 점이 생겼다면 꼭 댓글로 질문해주시고 도움이 되셨다면 공감이랑 구독 버튼 꾹 눌러주세요.
그럼 다음 포스팅에서 뵙겠습니다!
math is beatiful
'수학 > 여러가지 수학 공식 증명' 카테고리의 다른 글
| 피타고라스의 정리(Pythagorean theorem)의 여러가지 증명법(1) (0) | 2019.08.03 |
|---|